11480. Stock maximize

Your algorithms have become so good at predicting the market that now you know what the share price of Wooden Orange Toothpicks Inc. (WOT) will be for the next number of days.

Each day, you can either buy one share of WOT, sell any number of shares of WOT that you own, or not make any transaction at all. What is the maximum profit you can obtain with the optimum trading strategy?

Input. The first line contains the number of predicted prices n (1 ≤ n ≤ 50000) for WOT. The next line contains n integers p_i (1 ≤ p_i ≤ 10⁵), each is a predicted stock price on the i-th day.

Output. Print the maximum profit that can be obtained in the market.

Sample input 1	Sample output 1
4 1 4 2 3	4
Sample input 2	Sample output 2
9 5 2 6 9 1 6 5 8 3	26

SOLUTION

dynamic programming

Algorithm analysis

Let p₀, p₁, …, p_n-1 be the stock prices over the days. Compute dp_i = max(p_i, …, p_n-1) – the maximum on the suffixes of the array p. If we buy a share at price p_i on the i-th day, then in the future, we can profitably sell it at the highest price dp_i, gaining a profit of dp_i – p_i. We need to compute the total profit, which is equal to

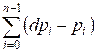
Example

Let’s consider the second test. Compute the maximum on the suffixes of the array of stock prices.

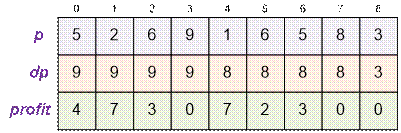
For example, on the first day, we buy a share for p₁ = 2, and later sell it for dp₁ = 9 (the sale will occur on the third day).

The total profit will be 4 + 7 + 3 + 0 + 7 + 2 + 3 + 0 + 0 = 26.

Algorithm realization

Read the input data.

scanf("%d", &n);

p.resize(n);

dp.resize(n);

for (i = 0; i < n; i++)

scanf("%d", &p[i]);

Compute dp_i = max(p_i, …, p_n-1).

dp[n - 1] = p[n - 1];

for (i = n - 2; i >= 0; i--)

dp[i] = max(p[i], dp[i + 1]);

Compute the total profit res. On the i-th day, we buy a share at price p_i, and later sell it for dp_i, gaining a profit of dp_i – p_i.

res = 0;

for (i = 0; i < n; i++)

res = res + dp[i] - p[i];

Print the answer.

printf("%lld\n", res);

Python realization

Read the input data.

n = int(input())

p = list(map(int, input().split()))

Compute dp_i = max(p_i, …, p_n-1).

dp = [0] * n

dp[n - 1] = p[n - 1]

for i in range(n - 2, -1, -1):

dp[i] = max(p[i], dp[i + 1])

Compute the total profit res. On the i-th day, we buy a share at price p_i, and later sell it for dp_i, gaining a profit of dp_i – p_i.

res = 0

for i in range(n):

res += dp[i] - p[i]

Print the answer.

print(res)